Sự giải thích chung về ánh sáng theo những nguyên lý này được khuếch đại bằng sự thảo luận cụ thể hơn về sự phản xạ và khúc xạ. Định luật phản xạ – rằng góc tới và góc khúc xạ bằng nhau – đã được người Hy Lạp biết đến; nhưng định luật khúc xạ—rằng các sin của góc tới và góc khúc xạ tỷ lệ với nhau tùy thuộc vào môi trường—hiện đã được xuất bản lần đầu tiên* Descartes coi đó là của riêng mình; nhưng dường như ông có những nghĩa vụ đáng kể với Willebrord Snell (sinh năm 1591, mất năm 1626), Giáo sư Toán học ở Leyden, người đã phát hiện ra nó bằng thực nghiệm (dù không phải ở dạng mà Descartes đưa ra) vào khoảng năm 1621. Snell đã phát hiện ra nó bằng thực nghiệm không công bố kết quả của mình mà truyền đạt nó dưới dạng bản thảo cho nhiều người, và Huygens khẳng định rằng bản thảo này đã được Descartes xem.

Descartes trình bày định luật như một sự diễn dịch từ lý thuyết. Tuy nhiên, điều này anh ta chỉ có thể làm được nhờ sự trợ giúp của phép loại suy;. khi các tia gặp vật thể có trọng lượng, “chúng có khả năng bị lệch hướng hoặc dừng lại giống như chuyển động của một quả bóng hoặc một hòn đá chạm vào vật thể”; vì ” thật dễ dàng để tin rằng hành động hoặc khuynh hướng chuyển động, mà tôi đã nói phải được coi là ánh sáng, phải tuân theo các định luật tương tự như chuyển động.” Do đó, anh ta thay thế ánh sáng, mà tốc độ truyền của nó mà anh ta tin là luôn luôn là vô hạn bởi một viên đạn có vận tốc thay đổi từ môi trường này sang môi trường khác. Định luật khúc xạ được chứng minh như sau* : —

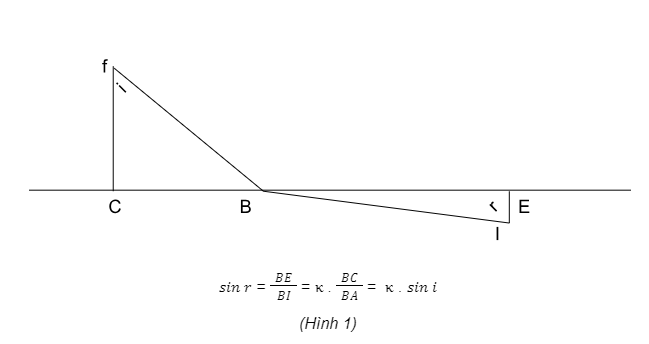
Cho một quả bóng ném từ A gặp một miếng vải CBE ở B, yếu đến mức quả bóng có thể xuyên qua nó và vượt ra ngoài, bong bóng với vận tốc tổng hợp của nó giảm theo một tỷ lệ xác định nào đó, chẳng hạn 1 : k.

Khi đó, nếu BI là độ dài đo được trên tia khúc xạ bằng AB, thì thời gian của viên đạn sẽ mất h lần thời gian để mô tả BI cũng như thời gian để mô tả AB. Nhưng thành phần vận tốc song song với tấm vải phải không bị ảnh hưởng bởi sự va chạm; và do đó hình chiếu BE của tia khúc xạ phải dài gấp k lần hình chiếu BC của tia tới. Vì vậy, nếu i và r biểu thị góc tới và khúc xạ, chúng ta có được: (Hình 1) hoặc sin của góc tới và góc khúc xạ tỉ lệ không đổi; đây là định luật khúc xạ.

Với mong muốn đưa tất cả các hiện tượng đã biết vào hệ thống của mình, Descartes dành sự chú ý nhất định đến một loại hiệu ứng mà vào thời điểm đó người ta ít nghĩ đến, nhưng chúng được dự đoán sẽ đóng một vai trò quan trọng trong sự phát triển tiếp theo của Vật lý.

Người xưa đã làm quen với những đặc tính kỳ lạ của hai loại khoáng vật là hổ phách và quặng sắt từ tính, loại trước khi cọ xát sẽ hút các vật nhẹ: loại sau có sức hút sắt.

Việc sử dụng nam châm nhằm mục đích chỉ hướng trên biển dường như không bắt nguồn từ thời cổ đại; nhưng nó chắc chắn đã được biết đến vào thời Thập tự chinh. Quả thực, từ tính là một trong số ít ngành khoa học phát triển trong thời Trung cổ; vì vào thế kỷ thứ mười ba Petrus Peregrinus* một người gốc Maricourt ở Picardy, đã có một khám phá có tầm quan trọng căn bản.

Lấy một nam châm tự nhiên hoặc đá nam châm đã được làm tròn thành dạng hình cầu, ông đặt nó lên một chiếc kim và đánh dấu đường mà chiếc kim tự đặt dọc theo đó. Sau đó đặt kim lên các phần khác của đá, anh ta thu được nhiều đường hơn theo cách tương tự. “Khi toàn bộ bề mặt của hòn đá được bao phủ bởi những đường như vậy thì tính chất chung của chúng trở nên rõ ràng; chúng tạo thành những vòng tròn bao quanh hòn đá giống hệt như các kinh tuyến bao quanh trái đất và có hai điểm ở hai đầu đối diện nhau.” về hòn đá mà tất cả các vòng tròn đều đi qua, giống như tất cả các kinh tuyến đi qua các cực Bắc Cực và Nam Cực của trái đất* Bị ấn tượng bởi sự tương tự, Peregrinus đề xuất gọi hai điểm này là các cực của nam châm: và ông quan sát thấy cách đó trong đó các nam châm tự đặt và hút nhau chỉ phụ thuộc vào vị trí các cực của chúng, như thể đây là trụ sở của lực từ. trong Triết học Tự nhiên.

Những quan sát của Peregrinus đã được mở rộng đáng kể không lâu trước thời Descartes của William Gilberd hoặc Gilbertf (b. 1540, d. 1603). Gilbert sinh ra ở Colchester: sau khi học tại Cambridge, ông theo học ngành y ở London và vinh dự được bổ nhiệm làm bác sĩ cho Nữ hoàng Elizabeth. Năm 1600, ông xuất bản một tác phẩm về Từ tính và Điện, từ đó bắt đầu lịch sử hiện đại của cả hai môn học.

Về những nghiên cứu về điện của Gilbert, chúng ta sẽ nói sau: trong từ trường, ông đã có khám phá cơ bản về lý do tại sao nam châm đặt theo những hướng nhất định so với mặt đất; nghĩa là bản thân mặt đất là một nam châm lớn, có một cực ở vùng cao phía bắc và cực kia ở vĩ độ cao phía nam. Do đó, tính chất của la bàn được coi là nằm trong nguyên tắc chung, đó là cực tìm kiếm phía bắc của mọi nam châm sẽ thu hút cực tìm kiếm phía nam của mọi nam châm khác và đẩy cực tìm kiếm phía bắc của nó.

Descartes đã cố gắng giải thích hiện tượng từ tính bằng lý thuyết xoáy của mình. Một vòng xoáy của chất lỏng là . xung quanh mỗi nam châm, vật chất của dòng xoáy đi vào từ một cực và rời ra ở cực kia: vật chất này được cho là tác dụng lên sắt và thép nhờ vào một lực cản đặc biệt đối với chuyển động của nó do các phân tử của những chất đó tạo ra.

Mặc dù hệ thống Descartes thô sơ có đặc điểm này và nhiều đặc điểm khác, nhưng chắc chắn rằng bằng cách đưa ra những quan niệm rõ ràng về hoạt động phân tử và áp dụng chúng cho một loạt các hiện tượng, nó đã kích thích tinh thần tìm hiểu và chuẩn bị đường cho những lý thuyết chính xác hơn được đưa ra sau đó. Vào thời của nó, nó đã nhận được sự chấp nhận rộng rãi: sự nhầm lẫn nảy sinh từ sự phá hủy trật tự cũ giờ đây dường như đã được kết thúc bằng việc tái tạo lại kiến thức trong một hệ thống vừa đáng tin cậy vừa đầy đủ. Ảnh hưởng của nó cũng không suy yếu nhanh chóng; vì ngay cả ở Cambridge nó đã được nghiên cứu rất lâu sau khi Newton công bố lý thuyết hấp dẫn của ông và vào giữa thế kỷ 18, Euler và hai người trong gia đình Bernoulli đã giải thích từ tính dựa trên giả thuyết về các xoáy.

Lý thuyết về ánh sáng của Descartes nhanh chóng thay thế các quan niệm thống trị thời Trung cổ. Tuy nhiên, giá trị giải thích của ông về khúc xạ đã bị người đồng hương của ông là Pierre de Fermat (i. 1601, d. 1665) nghi ngờ,§ và một cuộc tranh cãi xảy ra sau đó, được những người theo chủ nghĩa Descartes tiếp tục duy trì rất lâu sau cái chết của chủ nhân của họ. Fermat cuối cùng đã đưa ra một định luật cơ bản mới, từ đó ông đề xuất suy ra đường đi của tia sáng. Đây là Nguyên tắc Ít thời gian nhất nổi tiếng, được phát biểu* dưới dạng “Tự nhiên luôn hành động theo lộ trình ngắn nhất”. Từ đó có thể dễ dàng suy ra định luật phản xạ, vì đường đi được mô tả bởi ánh sáng giữa một điểm trên tia tới và một điểm trên tia phản xạ là ngắn nhất có thể phù hợp với điều kiện gặp các bề mặt phản xạ.f Để thu được định luật khúc xạ, Fermat cho rằng “điện trở của môi trường là khác nhau” và áp dụng “phương pháp cực đại và cực tiểu” của mình để tìm đường đi được mô tả trong thời gian ít nhất từ một điểm của một môi trường đến một điểm của cái khác. Năm 1661, ông đã tìm ra giải pháp.* “Kết quả công việc của tôi,” ông viết, “là điều phi thường nhất, điều không thể đoán trước nhất và hạnh phúc nhất từ trước đến nay; vì, sau khi thực hiện tất cả các phương trình, phép nhân, các phản đề, và các phép toán khác trong phương pháp của tôi, và cuối cùng khi giải quyết xong bài toán, tôi đã phát hiện ra rằng nguyên lý của tôi đưa ra một tỷ lệ chính xác và chính xác như nhau đối với các khúc xạ mà ông Descartes đã thiết lập.” Sự ngạc nhiên của ông còn lớn hơn nữa, vì ông đã cho rằng ánh sáng chuyển động chậm hơn trong môi trường đặc hơn so với trong môi trường hiếm, trong khi Descartes (như sẽ thấy rõ từ chứng minh ở trên) đã buộc phải đưa ra giả định trái ngược.

Mặc dù kết quả của Fermat là chính xác và thực sự có giá trị lâu dài, nhưng các nguyên tắc mà từ đó nó được rút ra đều mang tính chất siêu hình hơn là vật lý, và do đó ít được sử dụng cho mục đích đóng khung một cách giải thích cơ học về ánh sáng. Do đó, lý thuyết của Descartes đã được áp dụng cho đến khi cuốn Micrographia của Robert Hooke (sinh năm 1635, mất 1703), một trong những người sáng lập Hội Boyal, và từng là Thư ký của nó được xuất bản vào năm 1667§.

Hooke, vừa là nhà quan sát vừa là nhà lý thuyết, đã thực hiện hai khám phá thực nghiệm liên quan đến chủ đề hiện tại của chúng ta; nhưng trong cả hai điều này, có vẻ như anh đã được đoán trước. Đầu tiên là quan sát các màu óng ánh được nhìn thấy khi ánh sáng chiếu vào một lớp không khí mỏng giữa hai tấm kính hoặc thấu kính, hoặc trên một màng mỏng bằng bất kỳ chất trong suốt nào. Chúng thường được gọi là “màu sắc của tấm mỏng” hay “vòng Newton”; trước đây họ đã được Boyle quan sát. Khám phá thử nghiệm thứ hai của Hooke,}: được thực hiện sau thời kỳ Micrographia, là ánh sáng trong không khí không truyền chính xác theo đường thẳng mà có một số ánh sáng bên trong bóng hình học của một vật thể mờ đục. Quan sát này đã được công bố vào năm 1665 trong một tác phẩm để lại§ của Francesco Maria Grimaldi (b. 1618, d. 1663), người đã đặt tên cho hiện tượng này là nhiễu xạ.

Các nghiên cứu lý thuyết của Hooke về ánh sáng có tầm quan trọng rất lớn, thể hiện sự chuyển đổi từ hệ thống Descartes sang lý thuyết gợn sóng đã phát triển đầy đủ. Ông bắt đầu bằng việc công kích mệnh đề của Descartes, rằng ánh sáng là một xu hướng chuyển động hơn là một chuyển động thực sự. ” Có,” anh ấy nhận xét, || “không có Vật thể phát sáng nhưng có các bộ phận ít nhiều chuyển động” ; và chuyển động này “quá nhanh”. Hơn nữa, vì một số vật thể (ví dụ như viên kim cương khi bị cọ xát hoặc nung nóng trong bóng tối) tỏa sáng trong một thời gian đáng kể mà không bị lãng phí, nên bất cứ thứ gì đang chuyển động đều không bị mất đi vĩnh viễn đối với vật thể đó, và do đó chuyển động đó phải là của một nhân vật qua lại hoặc rung động. Biên độ của các dao động phải cực kỳ nhỏ, vì một số vật thể phát sáng (chẳng hạn như viên kim cương) rất cứng và do đó không thể bị uốn cong hoặc uốn cong ở bất kỳ mức độ nào có thể cảm nhận được.

Sau đó, kết luận rằng điều kiện liên quan đến sự phát xạ ánh sáng của một vật thể phát sáng là một chuyển động dao động nhanh có biên độ rất nhỏ, tiếp theo Hooke tìm hiểu xem ánh sáng truyền đi trong không gian như thế nào. “Điều tiếp theo chúng ta phải xem xét,” ông nói, “là cách thức hoặc cách thức chuyển động này xuyên qua cơ thể trong suốt đến mắt : Và ở đây điều đó sẽ dễ dàng được thừa nhận—

” Đầu tiên, nó phải là một cơ thể nhạy cảm và không thể thay đổi được chuyển động này thì mới xứng đáng được gọi là Minh bạch; và tiếp theo, các bộ phận của cơ thể đó phải đồng nhất hoặc cùng loại.

“Thứ ba, cấu tạo và chuyển động của các bộ phận phải sao cho sức đẩy của vật thể phát sáng có thể được truyền đi hoặc truyền qua nó đến khoảng cách lớn nhất có thể tưởng tượng được trong thời gian ít nhất có thể tưởng tượng được, mặc dù tôi thấy không có lý do gì để khẳng định rằng nó phải như vậy. ngay lập tức.

” Thứ tư, chuyển động được truyền theo mọi hướng thông qua một môi trường Đồng nhất bằng các đường thẳng hoặc thẳng kéo dài theo mọi hướng giống như các Tia từ tâm của Hình cầu.

Thứ năm, trong một môi trường đồng nhất, chuyển động này được truyền đi theo mọi hướng với vận tốc bằng nhau, do đó nhất thiết mọi xung hoặc rung động của vật thể phát sáng sẽ tạo ra một Quả cầu, quả cầu này sẽ liên tục tăng lên và lớn hơn theo cùng một cách (mặc dù nhanh hơn vô hạn). ) khi các sóng hoặc các vòng trên mặt nước phồng lên thành các vòng tròn lớn hơn và lớn hơn xung quanh một điểm của nó, nơi mà khi một hòn đá chìm xuống, chuyển động đã bắt đầu, từ đó nhất thiết phải tuân theo, rằng tất cả các phần của các Quả cầu này đều nhấp nhô thông qua một môi trường đồng nhất cắt các tia theo các góc vuông.”

Ở đây chúng ta có một quan niệm cơ học khá rõ ràng. Nó giống với Descartes trong việc công nhận một môi trường là phương tiện của ánh sáng; nhưng theo giả thuyết của Descartes thì sự nhiễu loạn là một áp suất tĩnh trong môi trường này, trong khi theo lý thuyết của Hooke thì đó là một chuyển động dao động nhanh với biên độ nhỏ. Ngoài ra, trong đoạn trích trên, Hooke còn giới thiệu ý tưởng về bề mặt sóng hoặc quỹ tích tại bất kỳ thời điểm nhiễu loạn nào được tạo ra ban đầu tại một điểm và khẳng định rằng đó là một hình cầu, có tâm là điểm đang nói đến và bán kính của nó là là các tia sáng phát ra từ điểm đó.

Nỗ lực tiếp theo của Hooke là tạo ra một lý thuyết cơ học về khúc xạ, để thay thế lý thuyết do Descartes đưa ra. ” Bởi vì,” ông nói, “tất cả các môi trường trong suốt đều không đồng nhất với nhau, do đó tiếp theo chúng ta sẽ xem xét xung hoặc chuyển động này sẽ được truyền như thế nào qua các môi trường trong suốt khác nhau. Và ở đây, theo nhà triết học Des sắc sảo và xuất sắc nhất.” Cartes, tôi cho rằng sin của góc nghiêng trong medium thứ nhất bằng sin khúc xạ trong giây, bằng mật độ của cái thứ nhất với mật độ của cái thứ hai. về trọng lực (trong đó độ khúc xạ hoặc độ trong suốt của môi trường không chiếm tỷ trọng), mà chỉ liên quan đến sự chuyển động của các Vịnh ánh sáng, trong đó chúng chỉ khác nhau ở điểm là xung truyền đi dễ dàng và yếu hơn, cái còn lại chậm hơn nhưng mạnh hơn.Nhưng đối với bản thân các xung, do khúc xạ, chúng sẽ có một tính chất khác mà bây giờ chúng ta sẽ cố gắng giải thích.

“Do đó, trong Hình đầu tiên, chúng ta giả sử ACFD là Tia vật lý, hoặc ABC a.m\BEF’ là hai Vịnh toán học, được truyền từ một điểm rất xa của vật thể phát sáng qua một môi trường trong suốt Đồng nhất LL, và DA , EB, FC, là những phần nhỏ của các xung quỹ đạo do đó phải cắt các Tia theo góc vuông: các Tia này gặp mặt phẳng NO của môi trường tạo ra sự truyền ánh sáng dễ dàng hơn và rơi xiên vào nó , trong môi trường MM chúng sẽ bị khúc xạ về phía vuông góc với bề mặt.Và vì môi trường này dễ bị dịch chuyển hơn môi trường trước 1/3 nên điểm U của xung quỹ đạo FC sẽ dịch chuyển đến H bốn không gian trong cùng một không gian. thời gian F, đầu kia của nó, được dịch chuyển sang ba khoảng trống, do đó toàn bộ xung khúc xạ tới H sẽ xiên với các tia khúc xạ CHK và GL” (Hình 2)

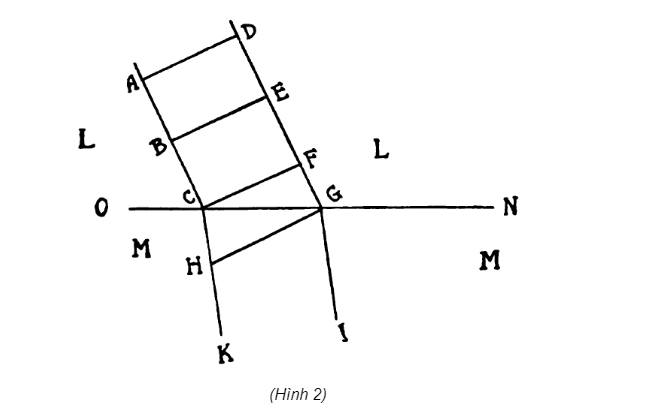
Mặc dù điều này không thành công ở mọi khía cạnh, nhưng nó thể hiện một bước tiến rõ ràng trong việc xử lý cùng một vấn đề của Descartes, vốn chỉ dựa trên một sự tương tự. Hooke cố gắng xác định điều gì xảy ra với mặt sóng khi nó gặp giao diện giữa hai phương tiện; và để đạt được mục đích này, ông đưa ra nguyên tắc đúng đắn rằng phía của mặt sóng gặp giao diện đầu tiên sẽ tiến về phía trước trong môi trường thứ hai với vận tốc phù hợp với môi trường đó, trong khi phía bên kia của mặt sóng vẫn ở trong môi trường thứ nhất vẫn chuyển động với vận tốc cũ nên mặt sóng sẽ bị lệch khi truyền từ môi trường này sang môi trường kia.

Sự lệch hướng của mặt sóng này được Hooke cho là nguồn gốc của các màu sắc lăng trụ. Ông coi ánh sáng tự nhiên hoặc ánh sáng trắng là loại nhiễu loạn đơn giản nhất, được tạo thành bởi một xung đơn giản và đều vuông góc với hướng truyền, và suy ra rằng màu sắc được tạo ra bởi sự biến dạng mà nhiễu loạn này phải chịu trong quá trình khúc xạ. . “Tia,”* ông nói, “bị phân tán, phân chia và mở ra do Khúc xạ của nó ở các Bề ngoài của môi trường thứ hai, và từ một đường được mở ra thành các Bề ngoài khác nhau, và do đó bị che khuất, nhờ đó tạo ra sự xuất hiện của các Màu sắc. .” “Màu sắc,” ông nói ở một nơi khác* “không gì khác hơn là sự nhiễu loạn của ánh sáng do sự truyền xung sang các môi trường trong suốt khác, tức là do sự khúc xạ của chúng.” Giả thuyết chính xác của ông về các màu sắc khác nhau là “Màu xanh lam là một ấn tượng trên Võng mạc về một xung ánh sáng xiên và hỗn tạp, phần yếu nhất đi trước và phần mạnh nhất theo sau. Và, màu đỏ đó là ấn tượng trên Võng mạc của một xung ánh sáng xiên và hỗn loạn, phần mạnh nhất đi trước và phần yếu nhất theo sau.”

(Còn tiếp …)